ブロードキャスト積
【英語版はこちら】
東京大学の松井です。名古屋工業大学の横田先生とブロードキャスト積「\(\boldsymbol{\mathcal{A}}\boxdot\boldsymbol{\mathcal{B}}\)」という新たな掛け算を提案しました。
概要
numpyにおいて行列とベクトルの要素積を計算する場合、ベクトルが行列と形状が揃うように自動的に複製されます。これはブロードキャストと呼ばれる機能です。
# A.shape == (3, 2)
A = np.array([[1, 2],
[3, 4],
[5, 6]])
# v.shape == (1, 2)
v = np.array([[7, 8]])
# Broadcast & multiply
A * v
# > array([[ 7, 16],
# > [21, 32],
# > [35, 48]])
一方で、通常の数式では当然ながらこのように書くことは出来ません。\(\mathbf{A} \in \mathbb{R}^{3 \times 2}, \mathbf{v} \in \mathbb{R}^{1 \times 2}\)とし、2つのテンソルの要素積(アダマール積)を\(\odot\)とすると、上記のnumpyの記述を直接書き下そうとして
\[\mathbf{A} \odot \mathbf{v} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix} \odot \begin{bmatrix} 7 & 8 \end{bmatrix}\]と書くことはできません。アダマール積の前後の行列・ベクトルの形状が揃わないからです。 ところが、近年のコンピュータビジョンの多くの論文ではこの点を無視してnumpyの式をそのまま記載する論文が非常に多いです。これは数学的に間違った議論となってしまうため、よくありません。
そこで、我々はnumpyにおけるブロードキャスト積を正しく表現してくれる演算子であるブロードキャスト積 \(\boxdot\)を提案します。ブロードキャスト積は、\(\boxdot\)の前後のテンソルについて、その形状が揃うように適切に要素を複製し、そのうえで要素積を計算します。ブロードキャスト積を用いると、上記の演算は次のように書けます。
\[\mathbf{A} \boxdot \mathbf{v} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix} \boxdot \begin{bmatrix} 7 & 8 \end{bmatrix} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix} \odot \begin{bmatrix} 7 & 8 \\ 7 & 8 \\ 7 & 8 \end{bmatrix} = \begin{bmatrix} 7 & 16 \\ 21 & 32 \\ 35 & 48 \end{bmatrix}\]このように、最初のnumpyと同じ結果を得ることができました。ブロードキャスト積を用いることで、numpyの表記を正しく数式で表現することが出来ます。
具体例
高さが\(H\)で幅が\(W\)であるRGB画像\(\boldsymbol{\mathcal{X}} \in \mathbb{R}^{H \times W \times 3}\)に対し、バイナリマスク\(\mathbf{B} \in \{ 0, 1\}^{H \times W}\)を適用し指定部位を抜き出し画像\(\boldsymbol{\mathcal{Y}} \in \mathbb{R}^{H \times W \times 3}\)を得る処理を考えます。多くの論文では、この処理は \(\boldsymbol{\mathcal{X}} \odot \mathbf{B} = \boldsymbol{\mathcal{Y}}\) と書かれます。
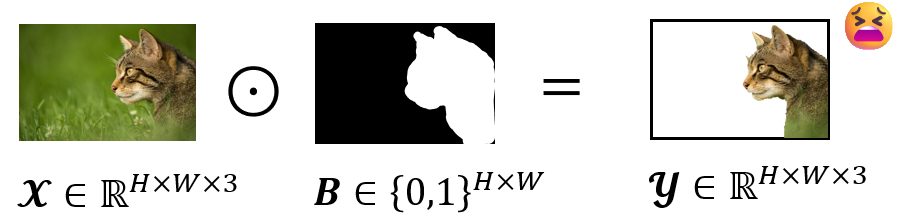
しかし、この処理は実は間違いです。なぜなら、テンソルの形状が違うため要素積が適用できないからです。これを正しく記述するならば、マスク\(\mathbf{B}\)をチャンネル方向に複製した新たなテンソルを定義する必要があります。しかしそれは煩雑です。ブロードキャスト積を用いれば、この処理を数学的に厳密に書き下せます。
\[\boldsymbol{\mathcal{X}} \boxdot \mathbf{B} = \boldsymbol{\mathcal{Y}}\]特性
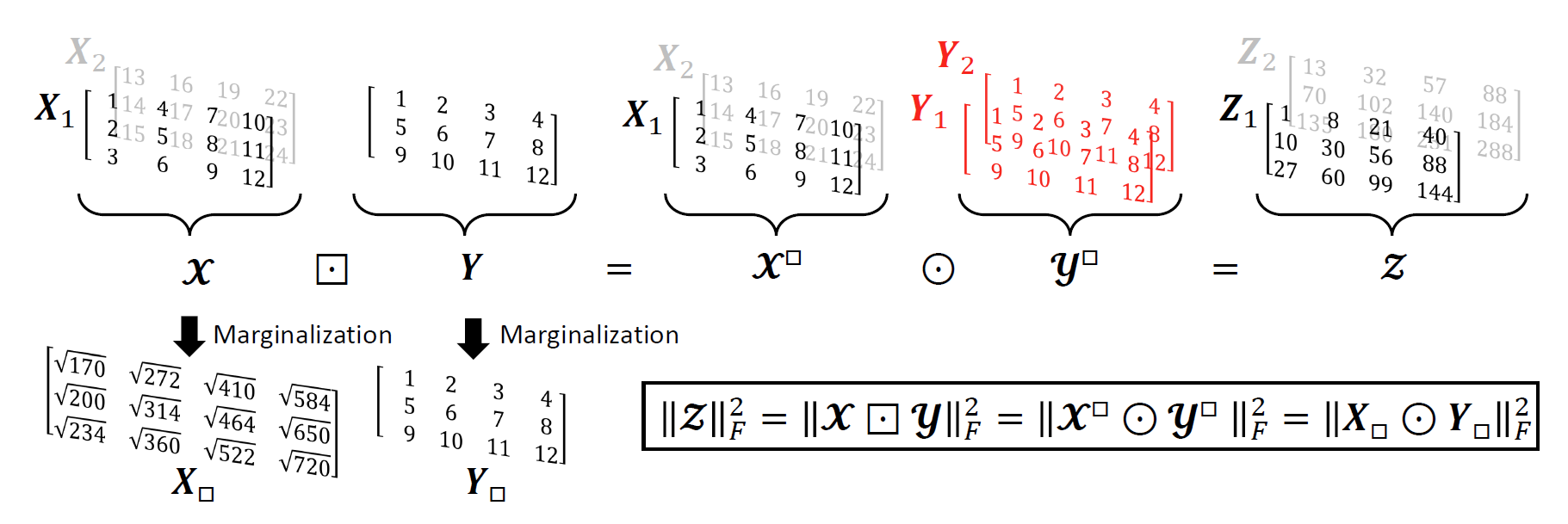
私達はこのブロードキャスト積に関し、周辺化やフロベニウスノルムに関する特性を導きました。詳細は論文をご覧ください。
最適化
さらに、私達はこのブロードキャスト積を用いた行列の近似を提案しています。すなわち、\(\boldsymbol{\mathcal{Y}} \in \mathbb{R}^{I \times J \times K}, \boldsymbol{\mathcal{A}} \in \mathbb{R}^{I \times J \times 1}, \boldsymbol{\mathcal{Z}} \in \mathbb{R}^{1 \times J \times K}\)に対し、次のような最小二乗問題の解を得ることができることを示しました。
\[\min_{\boldsymbol{\mathcal{A}}} \left\| \boldsymbol{\mathcal{Y}} - \boldsymbol{\mathcal{A}} \boxdot \boldsymbol{\mathcal{Z}} \right\|_F^2\]さらにこれを拡張することで、「ブロードキャスト積によるテンソル分解」が可能であることを示しました。
\[\boldsymbol{\mathcal{Y}} \approx \boldsymbol{\mathcal{A}} \boxdot \boldsymbol{\mathcal{B}} \boxdot \boldsymbol{\mathcal{C}}\]実験により、ある種の人工データに関しては、ブロードキャスト積による分解はCP分解やTucker分解よりも高い精度でテンソルを近似できることを示しました。これはブロードキャスト積はテンソル分解における新たな切り口となる可能性があることを示唆します。詳しくは論文をご覧ください。
是非使ってみてください!
是非ブロードキャスト積を使ってみてください!TeXでは \usepackage{amssymb}とした上で\boxdot と打てば記述できます。ブロードキャスト積を使うと、これまで曖昧だった部分が数学的に正確に記載できるだけでなく、これまで気付かなかった式変形を発見することができるかもしれません。
関連する文献
本論文はMIRU2024においてオーディエンス賞を受賞した「ブロードキャスト積:テンソル形状を揃えた要素積演算」に分量を追加し英訳したものになります。また、以下の過去のブログポストは本論文を着想するに至った背景になります。