Broadcast Product
I am Matsui from the University of Tokyo. Together with Professor Yokota from Nagoya Institute of Technology, we have proposed a new type of multiplication called Broadcast Product: \(\boldsymbol{\mathcal{A}}\boxdot\boldsymbol{\mathcal{B}}\).
Abstract
In numpy, when calculating the element-wise product of a matrix and a vector, the vector is automatically replicated to match the shape of the matrix. This feature is called broadcasting.
# A.shape == (3, 2)
A = np.array([[1, 2],
[3, 4],
[5, 6]])
# v.shape == (1, 2)
v = np.array([[7, 8]])
# Broadcast & multiply
A * v
# > array([[ 7, 16],
# > [21, 32],
# > [35, 48]])
On the other hand, in conventional mathematical notation, we cannot write the product in this way. Let \(\mathbf{A} \in \mathbb{R}^{3 \times 2}, \mathbf{v} \in \mathbb{R}^{1 \times 2}\), and denote the element-wise product (Hadamard product) of the two tensors by \(\odot\). Consider the following example where the above numpy description is directly written down.
\[\mathbf{A} \odot \mathbf{v} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix} \odot \begin{bmatrix} 7 & 8 \end{bmatrix}\]It is impossible to write the product this way because the shapes of the matrix and vector do not match. However, this point has often been ignored in many recent papers on computer vision, and the numpy notation is used directly. Such description leads to mathematically incorrect arguments.
Therefore, we propose the Broadcast Product \(\boxdot\), an operator that correctly represents the broadcast operations in numpy. The Broadcast Product replicates the elements of the tensors so that the tensors’ shapes match, then computes the element-wise product. Using the Broadcast Product, the above operation can be written as follows.
\[\mathbf{A} \boxdot \mathbf{v} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix} \boxdot \begin{bmatrix} 7 & 8 \end{bmatrix} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix} \odot \begin{bmatrix} 7 & 8 \\ 7 & 8 \\ 7 & 8 \end{bmatrix} = \begin{bmatrix} 7 & 16 \\ 21 & 32 \\ 35 & 48 \end{bmatrix}\]This way, we obtained the same result as the initial numpy description. Using the Broadcast Product, we can correctly express the numpy notation in mathematical form.
Example
Given an RGB image \(\boldsymbol{\mathcal{X}} \in \mathbb{R}^{H \times W \times 3}\) with height \(H\) and width \(W\), consider the process of applying a binary mask \(\mathbf{B} \in \{ 0, 1\}^{H \times W}\) to extract the foreground region and obtain the image \(\boldsymbol{\mathcal{Y}} \in \mathbb{R}^{H \times W \times 3}\). In many papers, this process is written as \(\boldsymbol{\mathcal{X}} \odot \mathbf{B} = \boldsymbol{\mathcal{Y}}\).
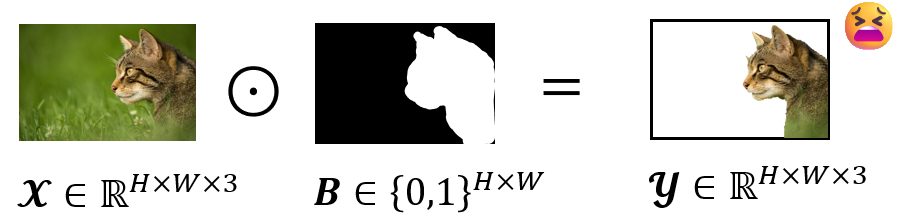
However, this process is incorrect because the element-wise product cannot be applied due to the mismatch in tensor shapes. To express this operation correctly, we need to define a new tensor by replicating the mask \(\mathbf{B}\) along the channel dimension, which is cumbersome. Using the Broadcast Product, this process can be written rigorously in mathematical terms.
\[\boldsymbol{\mathcal{X}} \boxdot \mathbf{B} = \boldsymbol{\mathcal{Y}}\]Properties
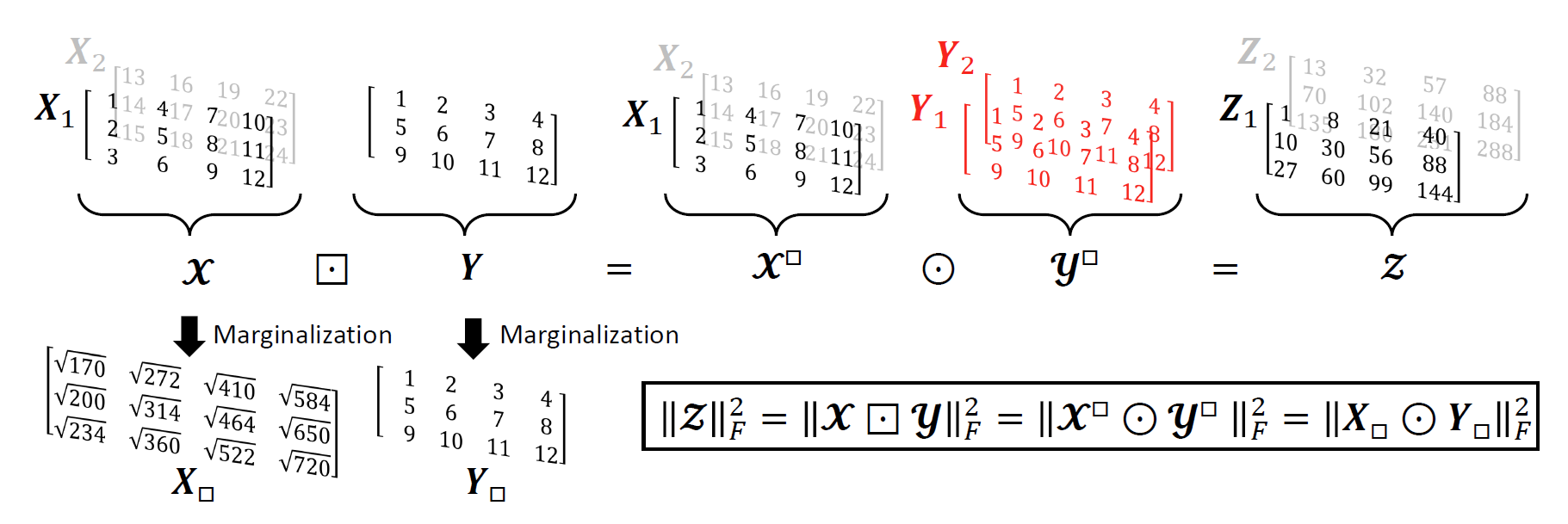
We have derived properties of the Broadcast Product about marginalization and the Frobenius norm. For more details, please refer to our paper.
Optimization
Furthermore, we propose a tensor approximation using the Broadcast Product. Specifically, for \(\boldsymbol{\mathcal{Y}} \in \mathbb{R}^{I \times J \times K}, \boldsymbol{\mathcal{A}} \in \mathbb{R}^{I \times J \times 1}, \boldsymbol{\mathcal{Z}} \in \mathbb{R}^{1 \times J \times K}\), we have shown that the solution to the following least squares problem can be obtained.
\[\min_{\boldsymbol{\mathcal{A}}} \left\| \boldsymbol{\mathcal{Y}} - \boldsymbol{\mathcal{A}} \boxdot \boldsymbol{\mathcal{Z}} \right\|_F^2\]Further extending this approach demonstrated that we can decompose a tensor using the Broadcast Product.
\[\boldsymbol{\mathcal{Y}} \approx \boldsymbol{\mathcal{A}} \boxdot \boldsymbol{\mathcal{B}} \boxdot \boldsymbol{\mathcal{C}}\]The experiment demonstrated that the Broadcast Product decomposition can approximate tensors more accurately than CP decomposition or Tucker decomposition for some synthetic data. This observation suggests that the Broadcast Product may offer a new perspective on tensor decomposition. For further details, please refer to our paper.
Please Give It a Try!
We encourage you to try using the Broadcast Product! In TeX, you can write \(\boxdot\) by \usepackage{amssymb} and \boxdot. Using the Broadcast Product, you can express previously ambiguous descriptions with mathematical precision. Further, you might uncover previously disregarded mathematical transformations that could lead to a new solution to your problem.