東京大学の松井と申します。本記事は壁 Advent Calendar 2025の12/20のものです。

集合が好きで、集合のことをずっと考えている。

tldr

c++の標準ライブラリおよびboostを用いる範囲で、集合を表す５つのデータ構造を紹介する
- std::set（赤黒木）
- std::unordered_set（クローズドアドレスのハッシュテーブル）
- boost::unordered_flat_set（オープンアドレスのハッシュテーブル）
- std::flat_setまたはboost::container::flat_set（ソート済み配列）
- boost::bloom（ブルームフィルタ）
壁ACベンチマークにより以下の示唆を得た
- 要素そのものを抽出しないで良い場合で、かつ疑陽性を許して良い場合は、boost::bloomが最速っぽい
- 一般にはboost::unordered_flat_setが最速っぽい
- boostが使えない場合はstd::unordered_setが無難
- std::setはstd::unordered_setより遅そう
- boost::container::flat_setは今回のベンチではstd::setと同じぐらいであったが、詳細は要検証

std::set（赤黒木）

C++では集合はstd::setというデータ構造で管理することが出来る。

std::set<std::string> kabe_set;

// データの挿入
kabe_set.insert("採択小噺");
kabe_set.insert("社論簡");
kabe_set.insert("楽元朗");

// データの検索
if (kabe_set.contains("採択小噺")) {
    std::cout << "採択小噺があるよ！" << std::endl;
}

std::setは赤黒木によって実装されているので、データの検索が \(O(\log N)\) で行える。logなので、爆速である。

std::unordered_set（クローズドアドレスのハッシュテーブル）

std::setは高速だが、一般により高速な std::unordered_set というものもある。

std::unordered_set<std::string> kabe_unordered_set;

// データの挿入
kabe_unordered_set.insert("採択小噺");
kabe_unordered_set.insert("社論簡");
kabe_unordered_set.insert("楽元朗");

// データの検索
if (kabe_unordered_set.contains("採択小噺")) {
    std::cout << "採択小噺があるよ！" << std::endl;
}

挿入と検索のインタフェースは同じである。std::unordered_setはクローズドアドレスのハッシュテーブルによって実装されており、検索が平均で \(O(1)\) である。定数なので、爆速である。

std::setもstd::unordered_setもc++の標準ライブラリに含まれており誰でもすぐ使える。一般にstd::unordered_setのほうが高速な場合が多いので、これを使っておけばとりあえず安心である。

さて、std::unordered_setは「クローズドアドレス」のハッシュテーブルである。クローズドアドレスとは、アイテムの衝突が発生したときの解決法を指す。wikipediaのハッシュテーブルの記事には以下のような図がある。

（上記画像はwikipediaのHash table/Separate chainingの記事である）

クローズドアドレスとは、最初にハッシュテーブルを習うときに出てくる衝突解決法である。ハッシュテーブルはアイテムをハッシュしてそれをキーとしてテーブルエントリを参照するものだが、もし２つのアイテムが同じキーを指してしまう（衝突）と困る。その際に、アイテムを後ろにポコポコつなげていくやり方がクローズドアドレスである。衝突が発生した場合、このポコポコつながったものを１つずつ見ていき、アイテムが存在すれば存在すると返す。なるほどである。

一方、オープンアドレスという衝突解決法もある。それが以下である。

boost::unordered_flat_set（オープンアドレスのハッシュテーブル）

オープンアドレスのハッシュテーブルの実装例としてはboost::unordered_flat_setがある。boostライブラリが必要である。インタフェースは同じである。

boost::unordered_flat_set<std::string> kabe_flat_set;

// データの挿入
kabe_flat_set.insert("採択小噺");
kabe_flat_set.insert("社論簡");
kabe_flat_set.insert("楽元朗");

// データの検索
if (kabe_flat_set.contains("採択小噺")) {
    std::cout << "採択小噺があるよ！" << std::endl;
}

オープンアドレスのハッシュテーブルとは、衝突が発生した際に、単純に次のスロットなどにエントリを入れてしまうというものである。強引である。

図を見るとわかりやすいだろう。以下がwikipediaの説明図である。

（上記画像はwikipediaのHash table/Open addressingの記事である）

また、以下の動画の説明もわかりやすい：

Andy Pavlo, “#07 - Database Hash Tables ✸ YugabyteDB Database Talk (CMU Intro to Database Systems)”

オープンアドレスはクローズドアドレスに比べて強引な印象があるが、実は高速である。衝突が発生したあと、単純に次のスロットを見に行くだけだからである。この操作は連続したメモリ領域にアクセスするのでキャッシュ効率がいい。現代のコンピュータのアルゴリズム設計においては、キャッシュ効率の良さは正義である。よって、オープンアドレスは一般にクローズドアドレスよりも高速になりがちであるらしい。ではなぜc++標準のstd::unordered_setではクローズドアドレスなのかというと、std::unordered_setなどが開発されたころはまだそのあたりの知見が十分ではなくクローズドアドレスのほうが一般的だったかららしい。このあたりについては、boost::unorderedの作者の方のブログ記事、およびboost::unorderedの公式ドキュメントが非常に詳しい。

また、boost::unordered_flatは、SIMD最適化前提のデータ構造となっている。これも高速化の一因である。

基本的に、検索性能に関していうとboost::unordered_flat_setはstd::unordered_setの上位互換なので、使えるときは使うといい。自分も最近の論文で使って、良い感じであった。

std::flat_set（ソート済み配列）

木やハッシュテーブルが高速なのはわかったが、集合を表すデータ構造として（データが比較可能で順序をつけられるのであれば）単にソートずみの配列を使って表し、探索時は二分探索で探してあげれば\(O(\log N)\)で要素を発見できて良さそうな気もする。そのようなデータ構造がstd::flat_setあるいはboost::container::flat_setである。

boost::container::flat_set<std::string> kabe_flat_set;

// データの挿入
kabe_flat_set.insert("採択小噺");
kabe_flat_set.insert("社論簡");
kabe_flat_set.insert("楽元朗");

// データの検索
if (kabe_flat_set.contains("採択小噺")) {
    std::cout << "採択小噺があるよ！" << std::endl;
}

この挙動については以下を参考にしてほしい。

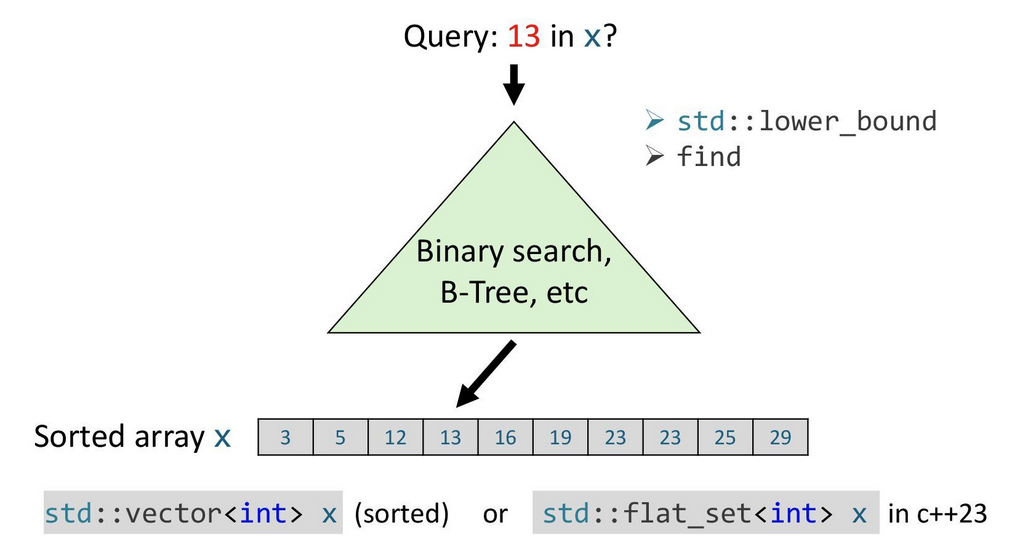松井勇佑、「学習型データ構造：機械学習を内包する新しいデータ構造の設計と解析」、p10

このデータ構造であると \(O(\log N)\)で検索ができてこれもまたシンプルで良さそうである。

また、「キーの範囲」というものが自明に抽出できて良さそうな気持ちにもなってくる。このデータ構造はboost::container::flat_setとしてboostライブラリで提供されており、そしてc++23ではstd::flat_setとして標準に含まれることとなった。とても新しいコンテナである。C++ Advent Calendar 2025の以下の記事でも紹介がされている。

@hon_no_mushi, “(C++23) flat_map: シンプルだが効率的なコンテナ”, C++ Advent Calendar 2025

メモリ効率がいいこと、キーに対するキャッシュ効率がいいことがうまみとのことである。

ここまでは集合を完全に保持するデータ構造の話であった。すなわち、要素を実際に取り出すことが可能なデータ構造であった。一方で、「要素の存在判定だけを行いたい（要素を取り出せなくてもいい）」場合、そして、多少の失敗があっても良い場合、より高速なデータ構造が存在する。それがbloom filterである。

boost::bloom（ブルームフィルタ）

ブルームフィルタは、boost 1.89からboost::bloomとしてboostに導入された。上記のboost::unordered_flat_setと同じ著者のJoaquínさん作である。熱いのである。

#include <boost/bloom_filter.hpp>
boost::bloom::filter<std::string, 2> kabe_bloom(100);

// データの挿入
kabe_bloom.insert("採択小噺");
kabe_bloom.insert("社論簡");
kabe_bloom.insert("楽元朗");

// データの検索
if (kabe_bloom.may_contain("採択小噺")) {
    std::cout << "採択小噺があるよ！" << std::endl;
}

ブルームフィルタは確率的なデータ構造だ。ビット配列を準備して、アイテムをハッシュして配列中のどこかに1を立てる、というような処理で集合を表現する。詳しくは次のスライドを参考にしてほしい。

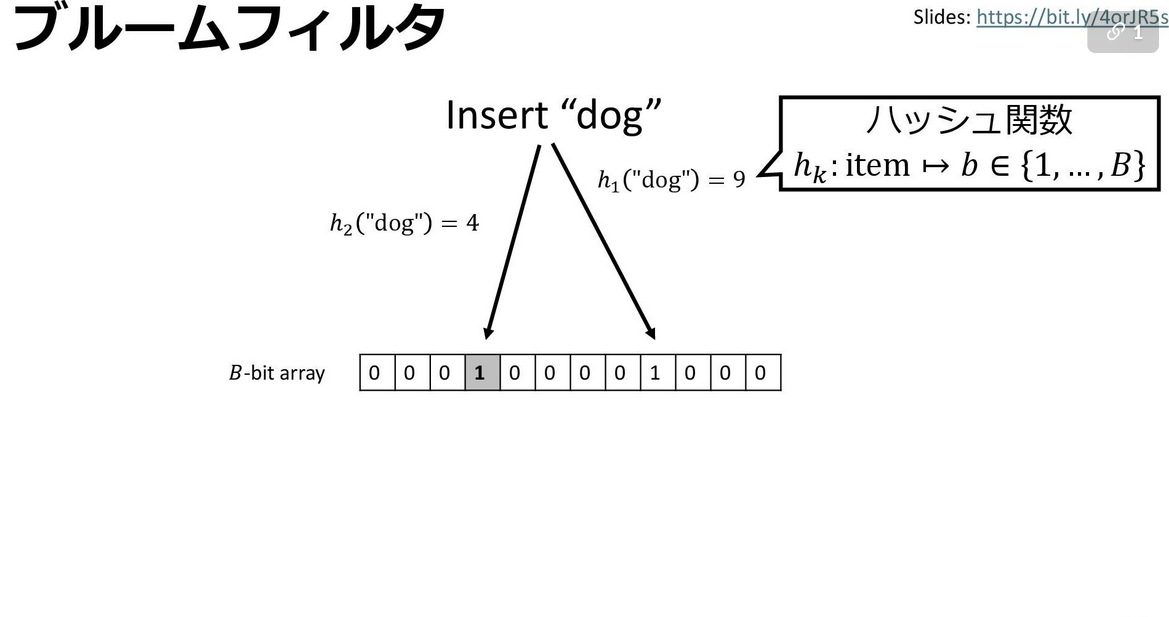松井勇佑、「学習型データ構造：機械学習を内包する新しいデータ構造の設計と解析」、p32

ブルームフィルタはアイテムそのものは保持しないので、たとえアイテムがクソデカ（たとえば1MBの画像）であっても、それを表現するのに数ビットしか使わないという異常な特性がある。しかも、ハッシュビットをたてるだけという挙動から、超高速である。このメモリ効率の良さと高速性の代償として、擬陽性が発生する。すなわち、ブルームフィルタに含まれているアイテムXに対しては、「Xがある？」と問い合わせると必ず「ある」と返してくれるが、含まれないアイテムYに対し「Yはある？」と聞くと、「無い」と答えてほしいところだがたまに「ある」と間違えて答えてくれるというものである。その弱点を理解して用いると、ブルームフィルタは大変便利である。

さて、ブルームフィルタはコンストラクションおよび検索のAPIが異なるので注意である。

boost::bloom::filter<std::string, 2> kabe_bloom(100);

上記において、「2」というのは使用するハッシュ関数の個数であり、「100」というのは、要素数ではなく、ビット配列のビット数である。このあたりの値を適切に決定する必要がある。

ここで、登場する変数を以下のように定めてみよう。

要素数：\(n\)
ビット配列のビット数：\(m\)（上でいう100）
ハッシュ関数の個数：\(k\)（上でいう2）
擬陽性率（Flase Positive Rate）：\(\mathrm{FPR}\)

ここで、\(n\)は自分のデータなので勝手に決まる。

ハッシュ関数の個数は \(k = \log_e 2 \cdot \frac{m}{n} \sim 0.693 \cdot \frac{m}{n}\)（を、整数に丸めたもの）とすれば擬陽性率が最小となってハッピーになることが知られている。

そして、擬陽性率（性能目標であり、低いほうがいい）は \(\mathrm{FPR} = \left ( \frac{1}{2} \right )^{\log_e 2 \cdot \frac{m}{n}} \sim {0.6185}^\frac{m}{n}\) で与えられる。

よって、ブルームフィルタの変数の設計方針としては基本的に次のどちらかになる。

メモリ使用量の要請により、ビット配列の長さ（\(m\)）を決める。たとえば要素数 \(n = 1000\) だとする。ここで、１要素あたり3ビットだとエイッと決めて \(m = 3 * 1000 = 3000\)とする。これにより、\(\mathrm{FPR} = {0.6185}^\frac{3000}{1000} = 0.237\)となり、疑陽性率は23.7%となる。　\(k = 0.693 \cdot \frac{3000}{1000} = 2.08\)より、ハッシュ関数の個数は2個と決まる（正確にはここで丸め誤差があるのでFPRは理想的なものにはならない）
許容できる疑陽性率（\(\mathrm{FPR}\)）をまず決める。例えば、要素数 \(n =1000\) として、\(\mathrm{FPR} = 0.1\)ということにする。そうすると \({0.6185}^\frac{m}{n} = 0.1\)より、\(m = 4.79n = 4790\)と決まる。よって、ビット配列の長さは4790ビットということになる。\(k = {0.693} \cdot \frac{4790}{1000} = 3.32\)より、ハッシュ関数の個数は3個程度と決まる。

ちなみに、もちろん\(k\)を先に決めてから\(m, \mathrm{FPR}\)を求めてもよい（\(k\)の丸め誤差が小さくなるように\(m\)を調整すると理論的には最適になる）が、\(k\)というのはデータ構造設計に際の直感的な量ではないかもしれない。

さて、面白いことに、上記の変数決定の議論では \(m/n\) という形で式が出てくるので、基本的に「要素あたり何ビット」という形の議論になる。イメージとして、10bit以下ぐらいを考えておくと良さそうである。また、データの性質を一切考えていないのに色々な関係が自動的に決まって不思議なのだが、これが確率的データ構造の面白いところなのである。

また、要素の検索にはmay_containというおしゃれな名前の関数を使う。上述の通り、この関数には疑陽性の可能性があるので注意。

用語について

一点、用語について注意がある。今回紹介したデータ構造は

set
unordered_set
flat_set
unordered_flat_set

となっており、

set -> unordered_setにパワーアップ
set -> flat_setにパワーアップ
unordered_setとflat_setを合体 -> unordered_flat_set

のような印象を抱くが、実態は 全く違い、それぞれ別のデータ構造である。この点だけは注意が必要である（というかわかりにくすぎんか？？？なんで？？）

ベンチマーク

さて、ベンチマークをとってみよう。詳細はここのリポジトリで公開している。

まず壁AC2015 - 2025の記事に含まれている単語を抽出したものがこれである。7524語の単語がある。

今回紹介した５つのデータ構造それぞれに対し、この7524個の単語を挿入しする。そして、それぞれのデータ構造に対し、

既に含まれている1000個の要素の検索
含まれていない1000個の要素の検索を行い、時間を計測する。

結果は以下である。（とてもおおざっぱな計測をしているので、あくまで傾向をつかむ程度の検証である）

=== std::set ===
Existing terms (1000 found): 226 μs
Non-existing terms (0 found): 192 μs

=== std::unordered_set ===
Existing terms (1000 found): 74 μs
Non-existing terms (0 found): 65 μs

=== boost::unordered_flat_set ===
Existing terms (1000 found): 32 μs
Non-existing terms (0 found): 14 μs

=== boost::container::flat_set ===
Existing terms (1000 found): 206 μs
Non-existing terms (0 found): 200 μs

=== boost::bloom::filter ===
Existing terms (1000 found): 11 μs
Non-existing terms (200 found): 18 μs

以下が知見である

boost::bloomが最速だが、擬陽性が200個発生している（擬陽性率23%程度で設定していたので、大体想定通りである）
その次に速いのはboost::unordered_flat_setである。boostを使える場合で、集合要素抽出も行いたい場合は、これを使うとよい。
std::unordered_setはその倍程度かかるが十分早い。boostを使えない場合はこれでいい。
std::setはその3倍くらい時間がかかったようだ。boost::container::flat_setは、今回のケースではstd::setと同程度であったが、要検証である。

他のライブラリ

ちなみに、集合を表すデータ構造はいろいろなライブラリに含まれている。googleのabseilやMetaのfollyが有名である。本記事執筆時点では、boost::unorderedシリーズが同等以上の性能を出しているようであった。また、boostは実質的に半分公式の標準ライブラリ的立ち位置であるので導入しやすいということもあるかもしれない。最新のデータ構造に常に注意を払っていきたい。

まとめ

boostは最近結構イケている。