はじめに

4-bit Product Quantization (4-bit PQ)は、2021年現在最も高速な近似最近傍探索アルゴリズムの１つです。 この度、Fixstars社と共同で、faissライブラリにおける4-bit PQのARM上での高速実装を達成し、faiss本家にマージされました。 本記事では、4-bit PQについて解説します。

4-bit PQは、PQという手法を近似し、SIMDレジスタによる恩恵を最大限に受けられるようにした方式です。以下では簡単のためVector Quantization (VQ)を対象とした、4-bit VQについて説明します。 VQを複数個並べたものがPQですので、4-bit VQと4-bit PQは大体同じだと思っていただいて大丈夫です。それでは解説を始めます。

ベクトル量子化による近似最近傍探索

\(N\)本の\(D\)次元データベースベクトル\(\mathbf{x}_1, \dots, \mathbf{x}_N\) があるとします。ここでクエリベクトル\(\mathbf{q} \in \mathbb{R}^D\) が与えられたときに、一番近いベクトルを近似的にでいいので探す処理を近似最近傍探索と呼びます。

ここでは特に、データベースベクトルが事前にベクトル量子化によって圧縮表現されている場合を考えます。すなわち、事前に\(K\)本のコードワードベクトル\(\mathbf{c}_1, \dots, \mathbf{c}_K\) を準備しておきます。そして、各\(\mathbf{x}\)について、最も近いコードワードを探し、 その添え字を\(k\)として保存します。以降、\(n\)番目のアイテムとして\(\mathbf{x}_n\)ではなく\(k_n\)だけを考えます。これを図示したものが以下です。

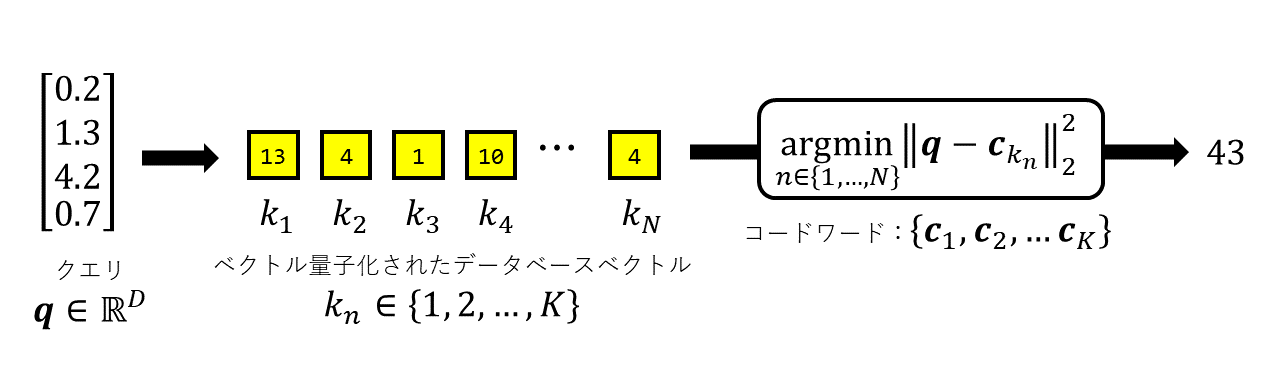
この表現は、データの大幅な近似表現です。すなわち、もとの\(\mathbf{x}_n\) は忘れてしまい、それに最も近いコードワードを\(\mathbf{x}_n\)の代わりだと思って 話をすすめるからです。 一方で、整数である\(k_n\)だけを保存すればよいので、 極めてメモリ効率がよいです。このようなベクトル量子化によるデータ圧縮表現は、 大規模データ探索で重要になります。詳しくはこちらをご参照ください。

さて、この表現のもと、どのように探索を行えばよいでしょうか？ 最も単純には、\(n\)番目のアイテムである\(k_n\)を考える際に逐一\(\mathbf{c}_{k_n}\)を 引っ張ってきて、\(\mathbf{q}\)と真面目に比べる（ユークリッド距離を計算する）ことができます。 しかし、これはベクトルを舐めるため少なくとも\(O(D)\)のコストがかかってしまいます。

実はここでは、最初に一回だけ距離表を作っておくと、それを用いて高速に計算できることが知られています。以下を見てみましょう。（距離表も次元も\(D\)で表していますが、関係はないです）

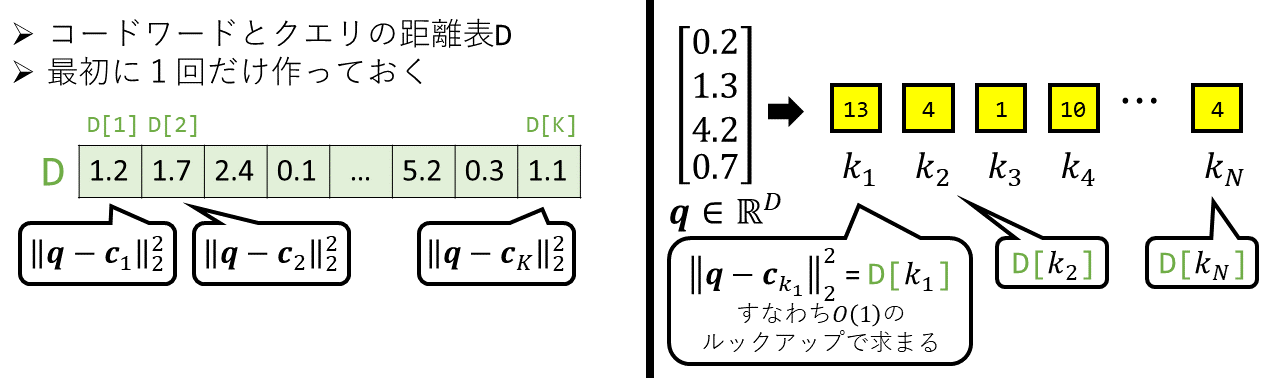
ここでは、距離表Dを作ります。この距離表の各要素は、クエリと各コードワードとの間の距離となっています。 このように、事前にクエリとコードワード間の距離を計算して保存しておくことで、 実際にアイテムたちとの距離を計算するときは、この距離表をルックアップするだけでよいことがわかります。すなわち、\(n\)番目のアイテムに対し\(O(1)\)のコストしかかかりません。 これがPQの元論文によって開発された有名な計算方式です。

これでOKなのですが、上記のルックアップはあくまでも「メモリに対するルックアップ」です。 よって、実はそこまで超高速ではないということが近年わかってきました。 この部分を「SIMDレジスタに対するルックアップ」に変更したものが、次に述べる4-bit VQになります。

SIMDを用いた高速計算

上記の表はどれくらいメモリを消費するでしょうか？次を見てみましょう。 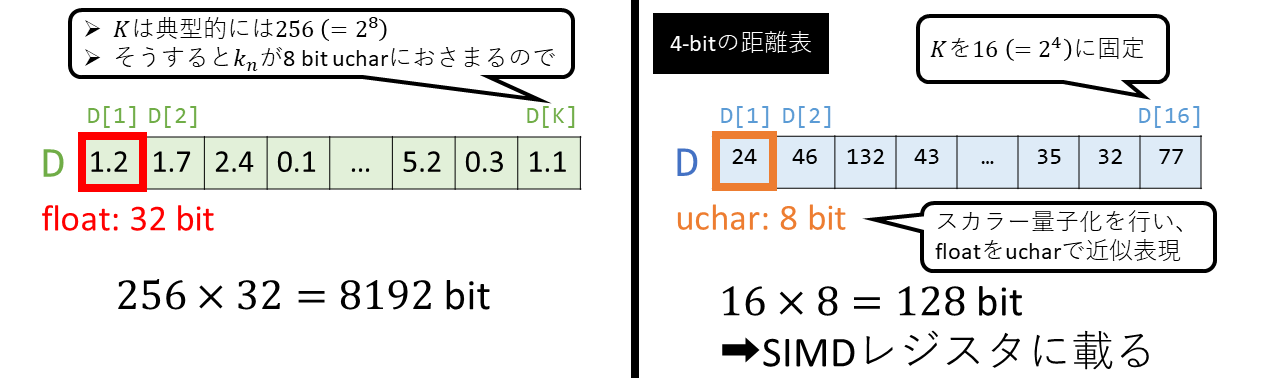通常、\(K\)は256とすることが多いです。これにより、\(k_n\)が8bitで収まり、扱いやすいからです。 そして、表の要素をfloatで表すとすると、これは結局8192 bitかかってしまいます。

ここで、上図の右のように、\(K\)を大胆に16とします。これにより、\(k_n\)は4bitでおさまります。 これが「4-bit VQ」の名前の由来です。 そして、floatだった各要素について、スカラー量子化を施すことで、8bitのucharで表現します（すなわち、とりうる値の最大最小を調べ、その範囲を等間隔に256分割して、整数を割り振ります）。 これにより、合計のメモリ消費が128bitにおさまります。

すると、これはSIMDレジスタに載ります。SIMDとは、スカラ要素をいくつかまとめて同時に処理できる ハードウェアおよび命令セットです。SIMD入門としては以下をご参照ください。

さて、話を戻すと、上記の処理により距離表が128bitになりました。これをSIMDレジスタに読み込みます。 そして、\(k_1\)から\(k_{16}\)までも同様にSIMDレジスタに読みます。 これを可視化したものが下図の上２つのSIMDレジスタになります。

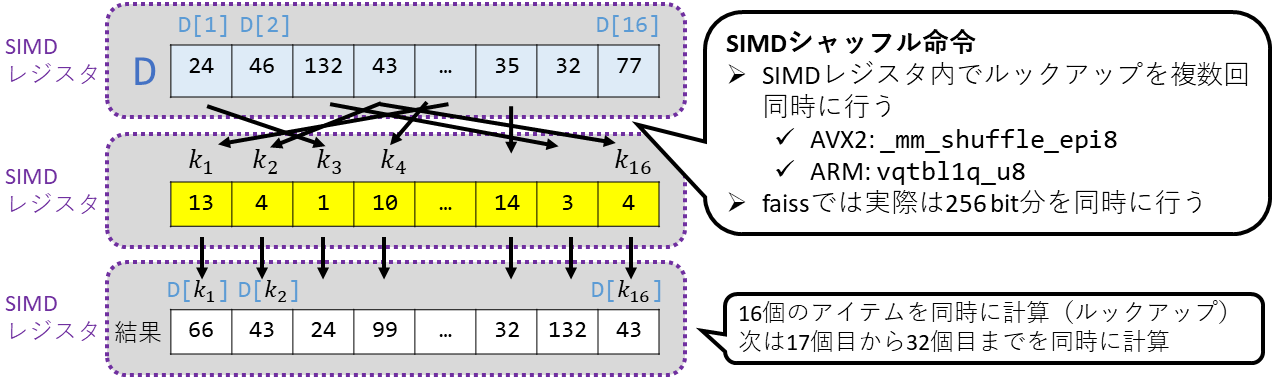
そして、ここでシャッフル命令を実行します。 シャッフル命令は、２つ目のレジスタの各要素が１つ目のレジスタの要素番号を 示し、その値を持ってくるというものです。それを、２つ目のレジスタの要素数分だけ 同時に行います。すなわち、ハッシュテーブルのルックアップを16並列で同時に行うということです。 これにより、上図の下のレジスタのように、最終結果がストアされます。 ちなみにここでは結果はスカラ量子化されているので、最終的に値を復元して終了となります。

さて、もともとの「メモリに対するルックアップ」に比べて、 「シャッフル命令を用いたSIMDレジスタに対するルックアップ」は比べ物にならないほど高速です。 そして、上記からわかる通り、16並列で実行することができます。 これが、もともとのVQに対して4-bit VQが精度を犠牲にする代わりに高速な探索を実現するキモとなります。

（ちなみに、上の議論だと各アイテムが4 bitで表されるので、16通りしか値を表現できないため、 そんなものは意味がないのではないかという疑問がわきます。それを解消するものが、VQを並べたPQと呼ばれる手法になります。）

技術の背景

さて、上記の4-bit PQの考え方は、もともとFabien Andréらによって考案されたものです。 コンピュータビジョン分野では探索手法は様々に提案されるものの、SIMDを絡めたような話は あまりありませんでした。Andréらはその中で、SIMDレジスタを有効活用する方式を提案しました。

そして、これらの内容は最近話題となったScaNNという手法でも取り入れられました

このScaNNの速度精度トレードオフでの強さは、SIMD実装に依るところが大きいそうです。

そして、これらを受けて、デファクトスタンダードなライブラリであるfaissにもSIMDの方式が取り入れられることとなりました。faissではIndexPQFastScanおよびIndexIVFPQastScanというクラスで利用が可能です。

ここ2010年代後半の近似最近傍探索は、HNSWをはじめとしたグラフベースの方式が盛り上がりを 見せていたのですが、4-bit PQの登場により、最高速度が必要な場合は4-bit PQという選択肢が 登場しました。今後はSIMDを絡めた話がさらに発展していくでしょう。

ARM実装とfaissへのマージ

さて、faissはもともとx86向けに作られており、ARMの対応はイマイチでした。 特にSIMDを多用する上記の4-bit PQは、そもそもARMにおけるSIMDコードが不十分であったため 十分な速度を実現できていませんでした。 そこで今回、私とfixstars社は共同でARM対応を行いました。 ARMは今後確実に伸びていく領域であるので、この部分でデファクトライブラリに 貢献することが出来たことは良かったです。自分自身、非常に勉強になりました。

詳細については今泉さんの記事を是非ご覧ください。

謝辞

本プロジェクトは、JSTさきがけ（JPMJPR1936）の支援を受けたものです。